matlab多自由度系统响应
在现代工程和科学研究中,多自由度系统的动态响应分析变得越来越重要。多自由度系统广泛应用于结构工程、机械系统、航空航天等领域,理解其动态特性对于设计和优化系统具有重要意义。在这方面,MATLAB作为一种强大的工具,提供了丰富的功能来分析和模拟多自由度系统。
多自由度系统是指具有多个运动自由度的系统,通常用来描述复杂的物理现象。例如,一座建筑物在地震作用下的响应,或者一架飞机在飞行中的稳定性,这些都可以被视为多自由度系统。与单自由度系统相比,多自由度系统能够更真实地反映实际情况,因而在工程应用中更为常见。
在MATLAB中,分析多自由度系统的响应通常涉及几个步骤:建模、求解和结果分析。首先,我们需要对所要分析的系统进行数学建模,确定其自由度、质量、阻尼和刚度等参数。对于多自由度系统,常用的模型是质量-弹簧-阻尼器模型,通过这些物理量的组合,我们可以形成系统的动态方程。
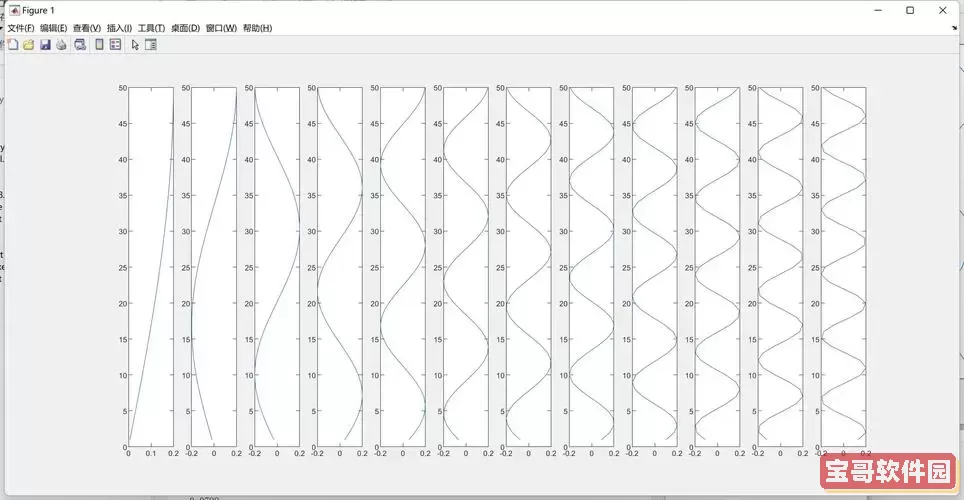
在MATLAB中,可以使用符号工具箱来构建这些方程。例如,我们可以用符号矩阵定义质量矩阵、刚度矩阵和阻尼矩阵。通过建立运动方程,我们可以将其转化为状态空间形式,便于后续的数值求解。
其次,求解步骤是通过数值方法来获取系统的响应。MATLAB提供了多种数值求解工具,比如“ode45”函数,它是解决常微分方程的强大工具。在定义好系统的运动方程后,我们可以调用ode45函数,输入初始条件和时间范围,即可得到系统的时域响应。
在分析多自由度系统时,我们还需要考虑输入信号的影响。常见的输入信号包括阶跃激励、脉冲激励和谐波激励等。在MATLAB中,可以使用各种函数生成这些输入信号,并将其与系统的响应进行叠加分析。这种功能使得我们可以评估系统在不同工况下的表现,从而进行更深入的研究。
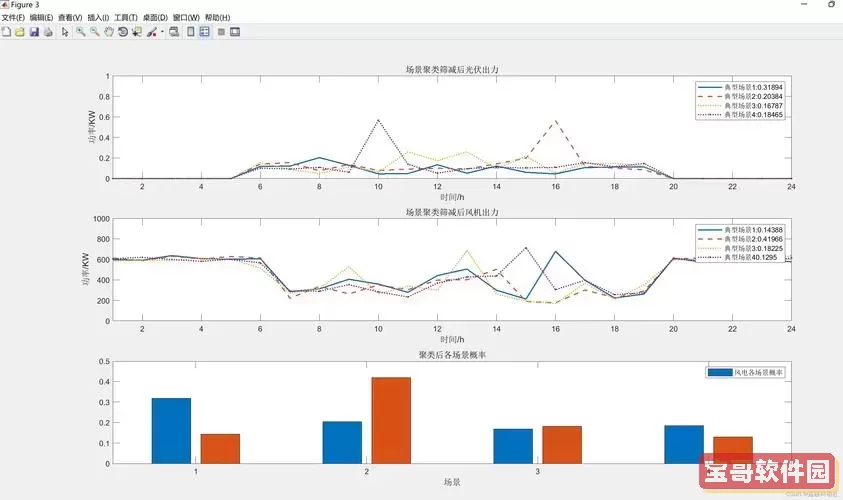
最后,结果分析阶段是整个过程的关键部分。通过绘图函数,如“plot”和“subplot”,我们可以直观地展示系统在不同输入条件下的响应特征。例如,我们可以绘制位移、速度和加速度随时间变化的曲线,通过观察这些曲线的形状、幅值和频率成分,能够快速判断系统的动态特性和稳定性。
此外,MATLAB还具有强大的数据处理和分析功能,能够对响应数据进行频域分析,如快速傅里叶变换(FFT)。通过分析系统的频率响应特性,可以深入了解系统的固有频率、阻尼比和振动模式等信息。这些都是设计和优化工程系统所不可或缺的依据。
综上所述,MATLAB为多自由度系统的响应分析提供了高效且灵活的工具,能够帮助工程师和研究人员更好地理解复杂系统的动态行为。在中国,随着智能制造和工程技术的不断发展,掌握MATLAB对于从事相关领域的专业人士而言,显得尤为重要。通过实践和不断学习,我们可以利用MATLAB更有效地解决实际问题,推动科技的进步和应用。
版权声明:matlab多自由度系统响应是由宝哥软件园云端程序自动收集整理而来。如果本文侵犯了你的权益,请联系本站底部QQ或者邮箱删除。